10.b: The Secret Code of Algorithm Complexity and Big O
Hey KISJ warriors! 🕵️♀️🕵️♂️ Remember that one time when you thought cramming the night before an exam was a good idea? It seemed simple until it wasn't. Well, in the digital world, algorithms sometimes face similar problems, and that's where the enigmatic Big O comes into play.
What is Big O Notation
- Think of Big O Notation like a fortune-teller for algorithms, predicting their future behavior without getting bogged down in the nitty-gritty.
The Ladder of Complexity
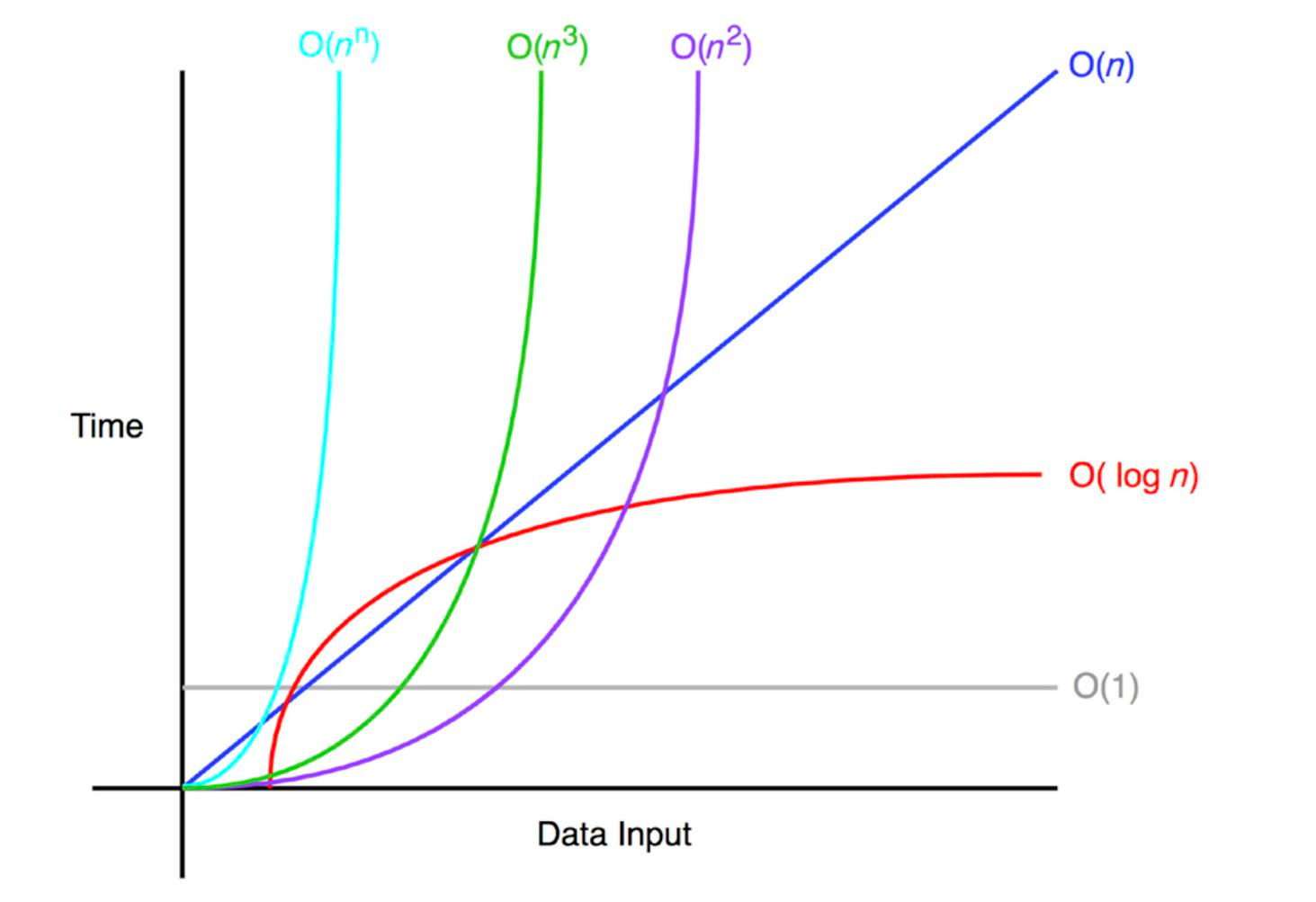
- Constant O(1): This one's chill. No matter how much data, it's like, "I got this."
- Linear O(n): More data, more time. Like standing in line at your favorite boba place.
- Logarithmic O(log n): The brainy one. It handles more data without breaking a sweat.
- Quadratic O(n^2): Things start heating up. More data means much more time.
- Cubic O(n^3): Like quadratic's big, intimidating cousin.
- Exponential O(2^n): The drama queen. A little more data, and it throws a major fit.
A Glimpse at Selection Sort
Picture sorting your playlist, dragging the best song to the start of the playlist and the second best to the second one and so on. That's kind of what Selection Sort does with data.
Steps:
- Scout the Smallest: Hunt down the tiniest number.
- Swap & Slide: Move it to the start.
- Rinse & Repeat: Do it again until everything’s sorted.
It’s like organizing your shoes but without the extra boxes. Everything gets swapped right where it is.
In this case, the complexity of this algorithm is O(n^2), so not the fastest when the party gets big. We will learn more "fancy" ones later!
Wrapping It Up
Just like understanding why your Wi-Fi turns into a sloth sometimes, getting the hang of algorithm complexity and champs like Selection Sort is key in the computing world. It's about being smart, efficient, and ready to tackle the big (and small) data challenges. So gear up because your coding journey's about to get a whole lot more interesting! 🚀👩💻👨💻





